Si Dawson . Com
The Trouble With Ratios
Ratios are used all over the place. No huge surprise there – they are, after all, just one number divided by another.
The well known problem case is when the denominator (the bottom bit) is zero, or very near zero. However, there are other subtler issues to consider.
Here’s a chart that has a ratio as the X axis:
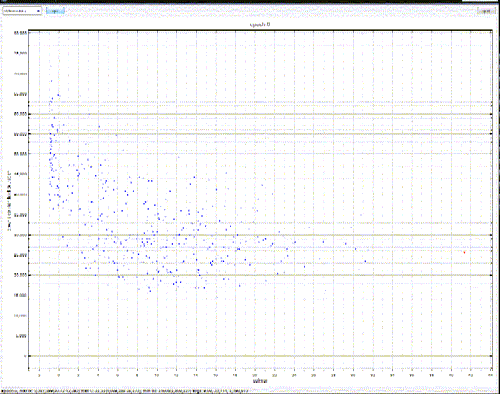
Don’t sweat the details, they’re not terribly important – just the rough distribution.
The X axis in this case is what’s called a Calmar – ie, the total dollar return of a system divided by it’s maximum drawdown. Or, in English – how much you make proportional to how big your pockets need to be. This gives a non-dollar based (ie, “pure”) number that can then be compared across markets, systems, products, whatever.
This graph is actually a bit trickier than that, since there’s actually 3 dimensions of data there – it’s just the third dimension isn’t plotted – but we’ll get back to that.
Where this gets ugly is when, in the case of the Calmar above, the drawdown drops to, or near to, zero. For example, if you have a system that only trades once – and it’s a winning trade – the calmar will be very, very large. Even if you chuck out systems that are obviously a bit nutty like that, you can still end up with situations where the ratio has just blown out of all proportion.
Which results in this:
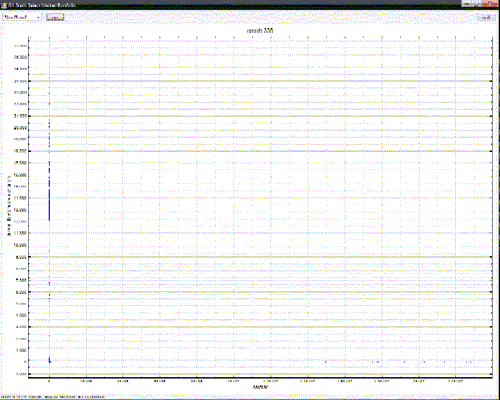
See how everything is in a vertical line on the left?
Well, it’s not. Those points are actually quite well spread out – it’s just that instead of the X axis going from 0->50 as in the first case, it now goes from 0->22 million – of which only a small number are greater than a hundred (you can see them spread out on the right, very close to the Y axis)
In this example, we can see the problem, so we’re aware of it. However, what if the ratio had been the unplotted third dimension? We might never have known.
Now, the way that I’m using these ratios internally, I’m protected from these sorts of blowouts – I simply compare sets of ratios. If one is bigger, it doesn’t matter if it’s bigger by 2 or by 2 billion.
However, there are many situations where you might want proportional representation. If one value is twice as big, say, it should occur twice as often. In this case, ratios that explode out by orders of magnitudes quickly swamp results, and drive the whole thing into the ground.
You swiftly end up with a monoculture. One result eats all the others, and instead of a room full of happy spiders doing their thing, you end up with one fat angry spider in the middle of the room. Umm, so to speak.
Ratios can be dangerous, kids. Watch out!